| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- SQL
- 그리디알고리즘
- 백트래킹
- Planned
- 파이썬
- 마라마라빔
- 프로그래머스
- Bellman-Ford
- 최소스패닝트리
- 알고리즘
- 장고
- minimum spanning tree
- 동적계획법
- DFS
- Kruskal
- B대면노래방
- MyPlaylist
- DP
- 종합설계
- 모각코
- 함밥
- django
- programmers
- BFS
- codetree
- 데이터베이스
- 실습
- 코드트리
- 소프트웨어공학
- 백준
- Today
- Total
Leta Learns
Segment Tree 본문
Segment Tree
: 사용자가 요청한 쿼리에 대해서 더 빠르게 응답하기 위해 만들어진 자료구조.
특정 기준으로 트리를 전처리하여 연산 속도를 높이게 된다.
이진 트리 구조. 구간 트리라고도 불림.
배열로 구현 가능.
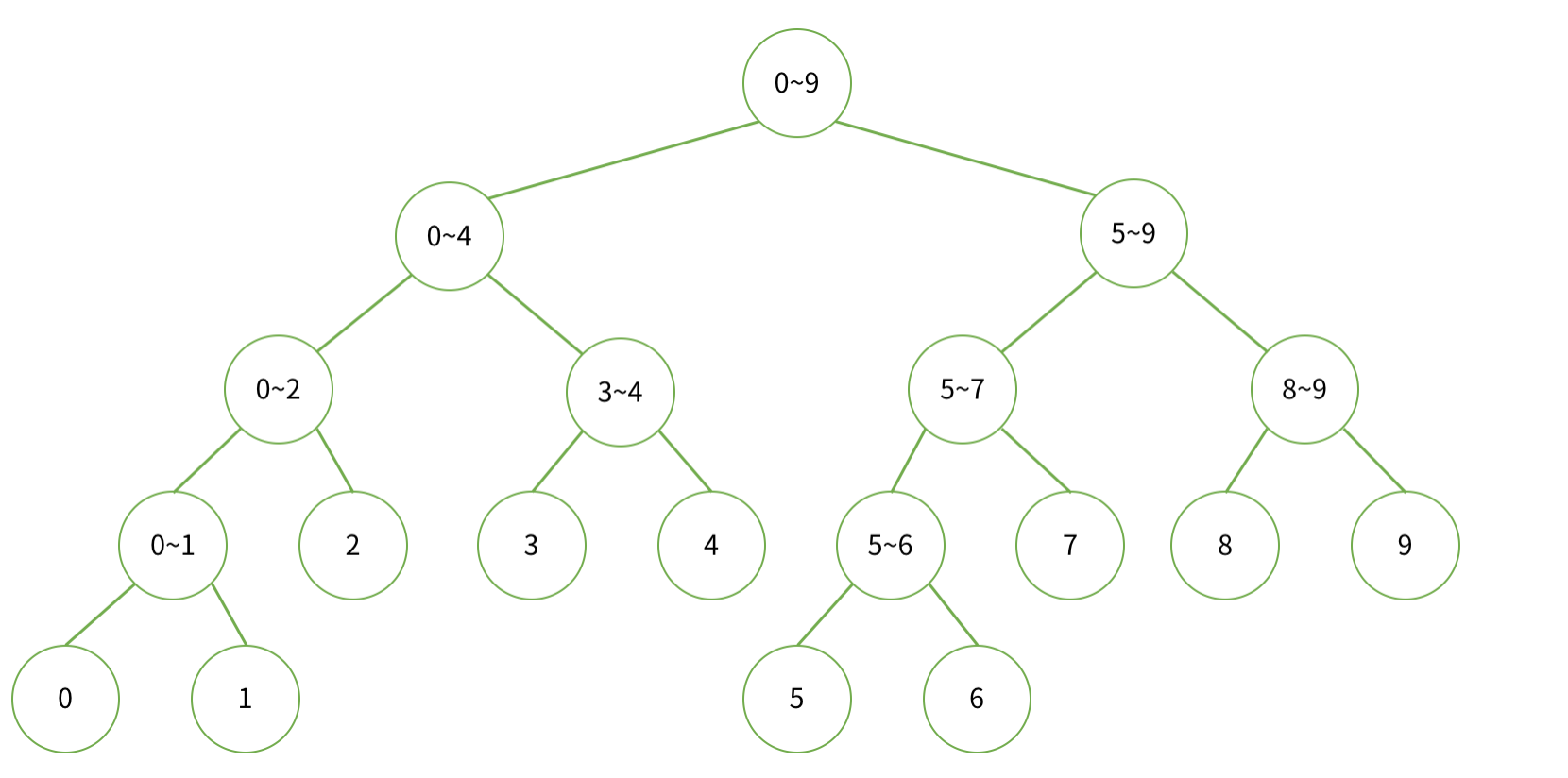
세그먼트 트리를 이루는 각 노드의 왼쪽 자식과 오른쪽 자식이 각각 해당 구간의 왼쪽 반과 오른쪽 반을 표현.
=> 이진 트리 구조
- Segment Tree를 사용하는 이유
배열 arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 있는 경우.
arr[4] + arr[5] + arr[6] 의 부분합을 구하는 쿼리와
arr[4]의 값을 바꾸는 쿼리가 있다고 하면
보통의 방식에서 부분합을 구하는 쿼리는 O(N), 값을 바꾸는 쿼리는 O(1)의 시간복잡도를 요구한다.
이처럼 수를 바꾸고 합을 구하는 연산이 M번 수행된다고 가정하면
총 O(MN + M) => O(MN)의 시간이 걸린다.
세그먼트 트리의 경우 이진 트리 구조를 가지고 있으므로
부분합을 구하는 쿼리에 O(logN), 값을 바꾸는 쿼리에 O(logN)의 시간복잡도가 요구된다.
이 경우에도 각 연산이 M번 수행된다고 가정하면
총 O(M logN + M logN) => O(M logN)의 시간이 걸린다.
=> 데이터가 많고, 반복 수행이 많아질수록 세그먼트 트리를 이용하는 것이 유용하다.
(훨씬 더 빠르게 쿼리를 수행할 수 있음)
- 예시
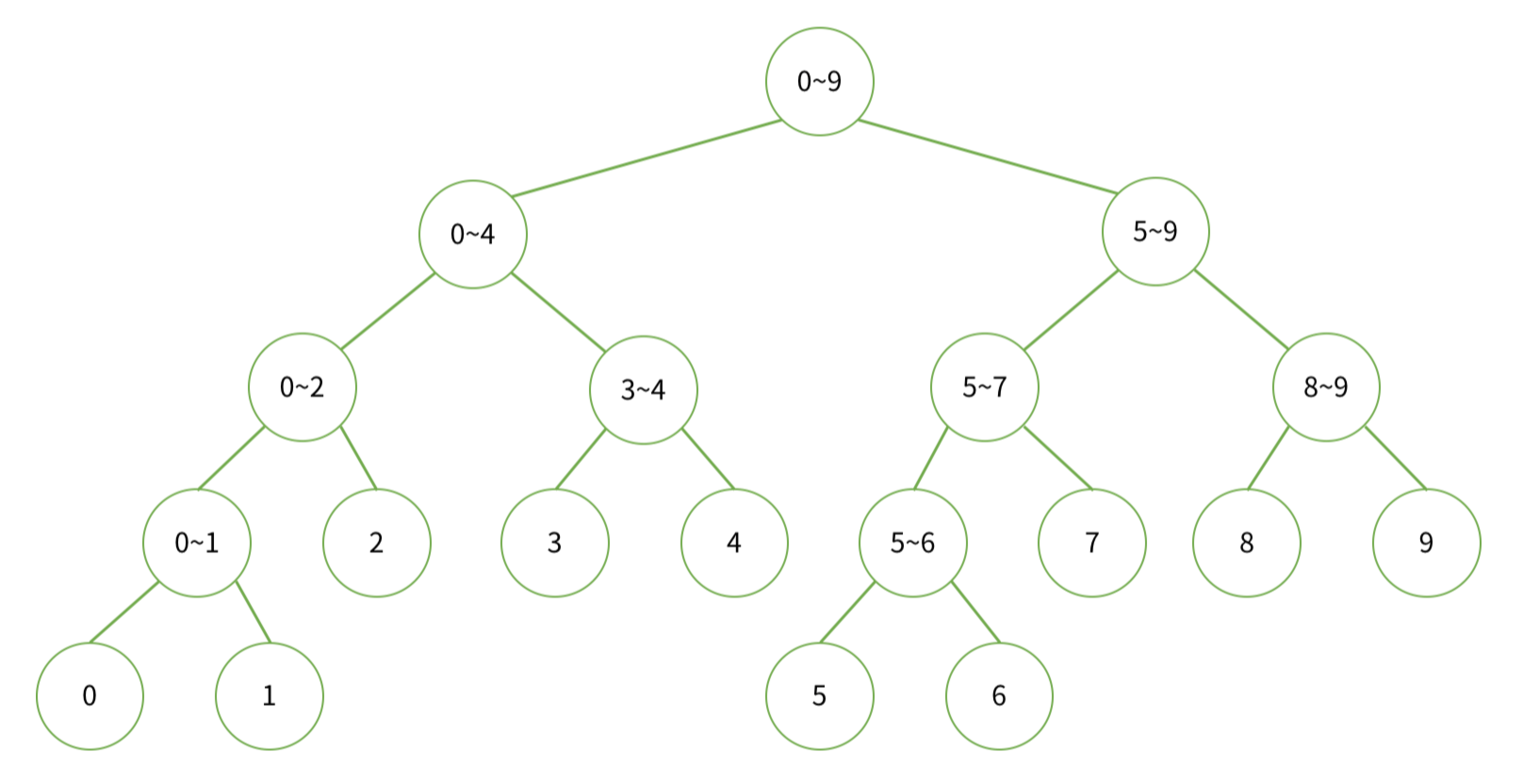
위 그림은 N=10인 경우 각 노드가 저장하고 있는 합의 범위를 나타낸다.
세그먼트 트리의 리프 노드는 구간의 길이가 1인 배열의 수 그 자체를 나타냄.
이외의 노드들은 왼쪽 자식과 오른쪽 자식의 구간합을 저장한다.
이진 트리 형태이므로 노드가 index 위치에 있다고 가정할 때,
노드의 왼쪽 자식은 index*2, 오른쪽 자식은 index*2+1.
# 초기화
def init(start, end, index):
if start == end: #leaf node인 경우
tree[index] = arr[start]
return tree[index]
mid = (start + end)//2
tree[index] = init(start, mid, index*2) + init(mid+1, end, index*2+1)
return tree[index]leaf node의 경우 배열의 수 그 자체를 가져야 하므로 tree[index] = arr[start]이다.
이외의 노드는 구간합을 저장해야 하므로
만약 해당 노드의 구간이 [start, end]라면 왼쪽 자식은 [start, (start+end)//2], 오른쪽 자식은 [(start+end)//2+1, end] 구간의 부분합을 나타내게 된다.
=> 재귀함수를 사용하여 왼쪽 자식과 오른쪽 자식의 트리를 만들고 합을 해당 노드의 인덱스에 저장한다.
# 부분합

(1): 겹치지 않으므로 더이상 탐색할 필요 x => 0 반환
(2): [left, right]가 [start, end]를 완전히 포함하므로 더이상 탐색할 필요 x => tree[node] 반환
(3), (4): 왼쪽 자식과 오른쪽 자식을 루트로 하는 서브트리로 이동하여 다시 탐색해야 함
def partial_sum(start, end, index, left, right):
if start > right or end < left:
return 0
elif start >= left and end <= right:
return tree[index]
else:
mid = (start + end)//2
return partial_sum(start, mid, index*2, left, right) + partial_sum(start, end, index*2+1, left, right)
# 값 바꾸기

어떤 수가 변경된다면 그 구간을 포함하는 모든 노드의 값을 갱신해야 한다.
index번째 수를 val로 변경한다면 그 변화량은 diff = val - a[index]이다.
노드가 담당하는 [start, end]에 index가 포함되는 경우 diff를 더해 합을 변경한다.
def update(node, start, end, index, diff):
if index < start or index > end:
return
tree[node] += diff
if start != end:
update(node*2, start, (start+end)//2, index, diff)
update(node*2+1, (start+end)//2+1, end, index, diff)
'Computer Science > Algorithm' 카테고리의 다른 글
| 오일러 경로, 회로 (Eulerian Trail) (0) | 2021.08.10 |
|---|---|
| LCA Algorithm (0) | 2021.07.30 |
| Dijkstra Algorithm (0) | 2021.07.30 |
| Bellman-Ford Algorithm (0) | 2021.07.28 |
| Tree DP, Bitmasking DP (동적계획법 심화) (0) | 2021.07.27 |




