Greedy Algorithm (그리디, 욕심쟁이 알고리즘)

 

1. Greedy Algorithm

    : 당장 눈 앞에 보이는 최적의 상황만을 쫓는 알고리즘

 

Greedy 알고리즘은 최적해를 구하는 상황에서 사용하는 방법이다.

여러 경우 중 하나를 선택할 때 그 상황에서 가장 좋다고 생각하는 것을 선택해 나가며 답을 구한다.

현재 상황에서 최선이라고 생각하는 것을 선택하는 방식이므로 가장 좋은 결과가 보장되는 것은 아니다.

 

출처 :  https://gomguard.tistory.com/119

위 그림의 경우, 가장 최적의 해는 연두색을 따라가서 얻는 결과인 107이지만 Greedy 알고리즘을 통해 값을 구하면 노란색을 따라가서 24라는 결과값이 나온다. 따라서 greedy 알고리즘이 최적해를 보장해주지는 않는다는 것을 알 수 있다.

 

But, 어느 정도 최적해에 근접한 값을 구할 수 있다.

 

 

 

 

 

2. Greedy Algorithm 예시

 

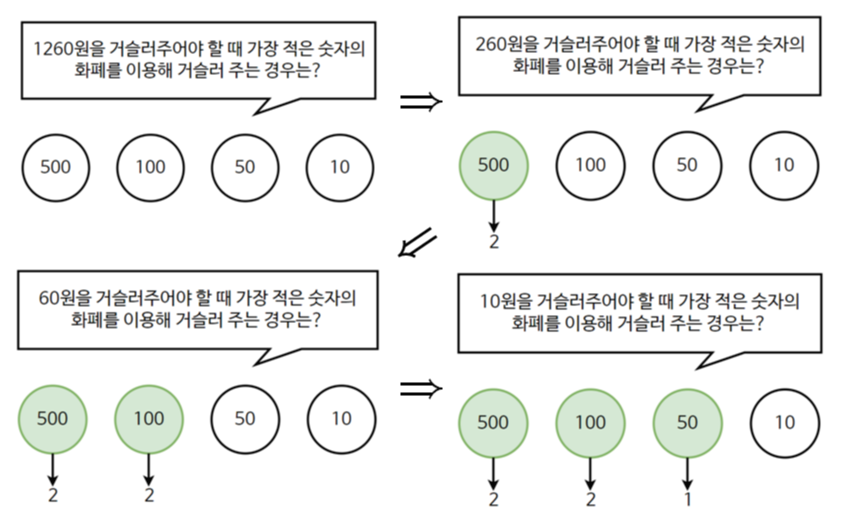
   <거스름돈 문제>

1260원의 거스름돈을 주어야 할 때 1원, 50원, 100원, 500원 동전을 사용하여 동전의 수가 가장 적은 경우로 지불하시오.

 

⇒ 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식.

  Greedy 알고리즘을 사용하여 매순간 최적, 최선이라고 생각되는 경우를 선택.

 

이 경우, ‘무조건 더 큰 화폐 단위부터 거슬러 준다’는 알고리즘을 지키면

  최적의 해 보장 가능.

 

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221242106787&proxyReferer=https:%2F%2Fwww.google.com%2F

출처 : https://m.blog.naver.com/PostView.nhn?blogId=ndb796&logNo=221242106787&proxyReferer=https:%2F%2Fwww.google.com%2F

 

 

 

 

 

3. Greedy Algorithm 한계

 

Greedy 알고리즘은 반드시 최적해를 구할 수 있는 방법은 아니다.

  따라서 근사치 추정에 활용된다.

  ⇒ 최적해에 가까운 값을 구하는 방법 중 하나이다.

 

Greedy 알고리즘을 사용하면 매 선택이 그 순간에 대해서는 최적이지만

종합적으로 봤을 때 최적이라는 보장은 절대 없다.

 

출처 : https://fullmoon1344.tistory.com/96