| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- MyPlaylist
- 최소스패닝트리
- Planned
- 소프트웨어공학
- 종합설계
- 알고리즘
- 동적계획법
- django
- B대면노래방
- 데이터베이스
- Bellman-Ford
- 백준
- 장고
- SQL
- minimum spanning tree
- 실습
- 코드트리
- 그리디알고리즘
- 파이썬
- 백트래킹
- programmers
- DP
- 프로그래머스
- 함밥
- 모각코
- BFS
- codetree
- DFS
- 마라마라빔
- Kruskal
Archives
- Today
- Total
Leta Learns
Union - Find (합집합 찾기) 본문
Union - Find (합집합 찾기)
- 대표적인 그래프 알고리즘
- 상호 배타적 집합 (Disjoint-Set) 알고리즘 (서로소 집합)
- 여러 개의 노드가 존재할 때 두 개의 노드를 선택하여, 이 두 노드가 서로 같은 그래프에 속하는지 판별
2가지 연산으로 이루어져 있다.
- Find : x가 어떤 집합에 포함되어 있는지 찾는 연산
- Union : x와 y가 포함되어 있는 집합을 합치는 연산
- 그림으로 이해하기
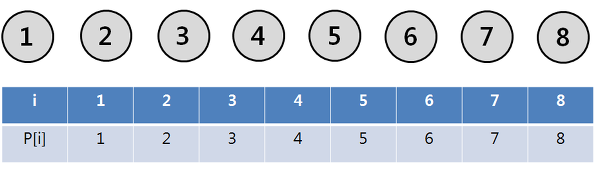
모두 연결되지 않고 각자 자기 자신만을 집합의 원소로 가지고 있을 때, 모든 값이 자기 자신을 가리키도록 만든다.
i : 노드번호
P[i] : 부모 노드 번호 ( => 자기 자신이 어떤 부모에 포함되어 있는지를 의미, parent)
지금 현재는 모든 값이 자기 자신을 가리키므로 P[i] = i 이다.

Union(1,2) Union(3,4)를 하여 노드를 연결하면,

i = 2 인 경우 P[i] = 1
i = 4 인 경우 P[i] = 3
=> 부모를 합칠 때는 일반적으로 더 작은 값 쪽으로 합친다.
=> 이를 '합침' Union 이라고 한다.
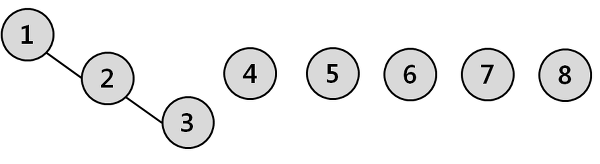
위와 같이 1, 2, 3이 한 그래프로 연결되는 경우에는 아래의 표처럼 표현이 된다.

i = 1, i = 3 이 두 경우는 부모가 다르기 때문에 (P[i]가 다름) 1과 3이 연결되었는지 파악하기 어렵다.
=> 재귀함수 사용
3의 부모인 2를 먼저 찾고, 2의 부모인 1을 찾으면 결과적으로 3의 부모는 1이 된다.
Union 연산을 수행하고 나면

위와 같은 표가 만들어진다.
i = 1, 2, 3 모두 P[i] = 1이므로 이 세 노드는 같은 그래프에 속한다는 것을 알 수 있다.
참고 : https://brenden.tistory.com/33
https://blog.naver.com/ndb796/221230967614
'Computer Science > Algorithm' 카테고리의 다른 글
| Bellman-Ford Algorithm (0) | 2021.07.28 |
|---|---|
| Tree DP, Bitmasking DP (동적계획법 심화) (0) | 2021.07.27 |
| Kruskal Algorithm (0) | 2021.07.21 |
| Prim Algorithm (0) | 2021.07.21 |
| Minimum Spanning Tree (최소 신장 트리) (0) | 2021.07.21 |
Comments




